В.В. Аполлонов, В.А. Ямщиков

 

К   ВОПРОСУ  ОБ  ЭФФЕКТИВНОСТИ   ЭЛЕКТРОРАЗРЯДНОГО   N₂ - ЛАЗЕРА

 

Рассмотрена зависимость эффективности N₂ - лазера от основных параметров самостоятельного разряда, электрической схемы возбуждения и газовой смеси. Экспериментально показано, что энергия излучения пропорциональна мощности накачки активной среды в момент, когда напряжение на плазме самостоятельного разряда максимально. Установлено, что максимальная энергия генерации достигается при таком давлении азота, когда максимальные мощность накачки и напряжение на плазме реализуются одновременно. Определена зависимость эффективности лазера от параметра ZC. характеризующего длительность импульса генератора накачки.

 

 

Электроразрядный лазер на переходах молекулы азота - перспективный источник излучения ближнего УФ диапазона. Такие лазеры широко применяются в микроэлектронной промышленности, медицине, лазерной химии, для накачки лазеров на органических красителях, в спектроскопических исследованиях, в лазерной диагностике плазмы и в других целях [1]. Его конструкция сравнительно проста, а рабочая среда химически инертна. Кроме того, для ряда применений длина волны азотного лазера оказывается наиболее эффективной.
Недостатком азотного лазера является его низкий КПД. Разброс КПД, приводимых в различных работах, очень велик: от 0,02 % [2] до 0,8 -1 % [3,4] при отсутствии принципиальных различий в конструкциях лазеров и без приемлемого объяснения причин таких расхождений. Попытки математического моделирования процессов, происходящих в азотном лазере, обычно касаются частных случаев [5,6] или же не дают удовлетворительного согласия с экспериментом. Это затрудняет поиск условий повышения КПД и создания лазеров с планируемыми характеристиками. В такой ситуации необходимо прямое исследование зависимости эффективности азотного лазера от базовых характеристик разряда, параметров схемы накачки, давления и состава газовой смеси, что и являлось целью настоящей работы.
Электрическая схема лазера, на котором проводились эксперименты, подобная схеме, описанной в [7], показана на рис.1а.

 

 

 

 

 

 

 

 

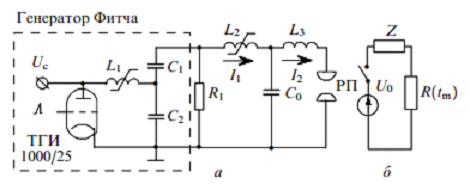
Рис. 1. Электрическая (а) и эквивалентная (б) схемы лазера.

 

 

 

Она состоит из LС- генератора Фитча, насыщающегося дросселя L₂ и обостряющей емкости C₀ , распределенной вдоль разрядного промежутка. Емкости С₁ и C₂ равны 20 нФ каждая. Обостряющая емкость равна ударной емкости генератора Фитча: С₀ = С₁/2 = 10 нФ. Обмотка дросселя L₂  выполнена в виде двойной металлической трубы, между стенками которой находятся ферритовые кольца с общей площадью сечения S = 67 см². Схема позволяет генерировать импульсы напряжения до 40 кВ с фронтом нарастания 80 нс. Разрядный промежуток (РП) размером 20 x 20 x 500 мм был образован двумя профилированными электродами. Расстояние между электродами d = 20 мм. PП подсвечивается УФ излучением от 50 искровых зазоров. Резонатор лазера состоит из кварцевой пластинки и глухого плоско-параллельного зеркала.
Эксперименты проводились при постоянном зарядном напряжении U_c = 20 кВ. На рис.2 приведены типичные осциллограммы импульсов напряжения U(t) на разрядном промежутке, тока /(t) через обостряющую емкость и импульса генерации N₂- лазера J(t).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

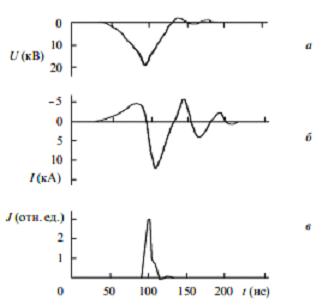
Рис.2. Осциллограммы импульсов напряжении (а), тока через емкость С₀ (б) и излучения лазера (в) для N₂- лазера при р_N2 = 120 мм рт.ст., U_c = 20 кВ.

 

 

 

На рис.З и 4 показаны экспериментальные зависимости максимального напряжения U_m на PП и энергии генерации W лазера на азоте и смеси азота с SF₆ (20 мм рт.ст.) от давления азота p_N2.

 

 

 

 

 

 

 

 

 

 

 

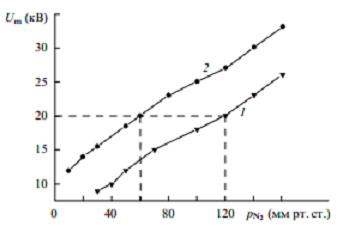
Рис.З. Зависимости максимального напряжения на разрядном промежутке U_m от p_N2 в лазерах на N₂ (1) и смеси N₂ - SF₆ (2).

 

 

 

 

 

 

 

 

 

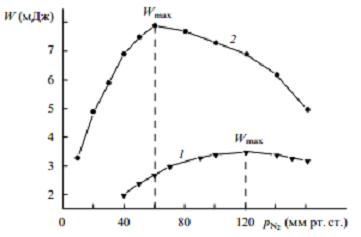
Рис.4. Зависимости энергии излучения W лазеров на N₂ (1) и смеси N₂ - SF₆ (2) от p_N2 (p_SF6 = 20 мм рт.ст.).

 

 

 

 

Зависимость отношения Е_m/р = U_m/pd, характеризующего температуру электронов в разряде (где Е_m - максимальная напряженность электрического поля, р = p_N2 + p_SF6 - полное давление газовой смеси), от p_N2  показана на рис.5.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

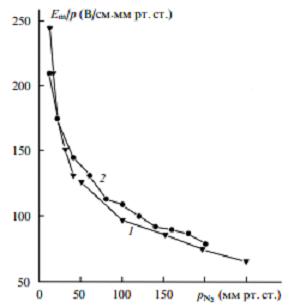
Рис.5. Зависимости отношения максимальной напряженности электрического поля в разряде к полному давлению газовой смеси Е_m/р от p_N2, в лазерах на N₂ (1) и смеси N₂ - SF₆ (2) (p_SF6 = 20 мм рт.ст.).

 

 

Существует распространенная точка зрения [4,8,9], что характеристики излучения N₂- лазера зависят, прежде всего, от отношения Е_m/р. Однако из рис.З и 5 видно, что в диапазоне рабочих давлении лазера изменение параметра Е_m/р не оказывает заметного влияния на поведение W.
Особенностью режима накачки N₂- лазера, как следует из рис.З и 5, являются низкие по сравнению с максимальным напряжением генератора Фитча (2U_с = 40 кВ) значения U_m, а также высокие значения Е_m/р в раз­ряде, которые намного больше порога ионизации азота E_i/p = 40 В/см*мм рт.ст. Это означает, что ионизация в РП и накачка активной среды начинаются раньше, чем достигается максимум напряжения на плазме, при этом через емкость С₀ одновременно текут ток заряда  /₁ и ток разряда /₂ (рис.1,а). Условие пробоя (максимальное напряжение U_m на РП) записывается в виде C₀dU(t)/dt = /(t) = /₁—/₂ = 0, т.е. /₁ = /₂. Как видно из рис.2.б, для p_N2 = 120 мм рт.ст. ток разряда составляет около 4 кА при максимальном напряжении на плазме 20 кВ.
Схему рис.1.а можно свести к еще более простой эквивалентной схеме [10] (см. рис.1,б). Здесь R(t_m) - сопротивление плазмы самостоятельного разряда в момент времени t_m , соответствующий максимуму напряжения на РП, Z- эквивалентное сопротивление электрической схемы, равное сопротивлению в режиме короткого замыкания РП, которое в общем случае может быть комплексным и содержать активную и реактивную составляющие. U₀ - напряжение эквивалентного генератора в режиме холостого хода на РП. Тогда пиковую мощность накачки в момент времени t_m можно определить из формулы

 

Р_m = I_mU_m = (U₀ - U_m) U_m /Z.                (1)

 

С увеличением давления азота U_m увеличивается (рис.З,а), поэтому согласно (1) мощность Р_m сначала будет возрастать, а затем убывать, достигая максимума в точке U_m = U₀/2 (при условии dP_m/dU_m = 0):

 

Р_maх = U₀²/4Z.     (2)

 

Поскольку используется генератор Фитча, то под U₀ следует понимать удвоенное зарядное напряжение: U₀ = 2 U_c.
Как видно из рис.З и 4, имеется однозначное соответствие между U_m и W. Используя это соответствие и формулу (1), можно построить зависимости W от Р_m, которые приводятся на рис.6 для условий наших экспериментов:        

 

Z ≈ (2(L_2s + L₃)/C₀ )^1/2 = 5 Ом, L_2s = 113 нГн

Здесь L_2s - индуктивность первого контура в режиме насыщения L₂. L₃ = 6 нГн, U₀ = 40 кВ. Из рис.6 хорошо видно, что W пропорционально Р_m. Стрелками обозначены участки подъема (слева направо) и спада (справа налево) для Р_m и W.

 

 

 

 

 

 

 

 

 

 

 

 

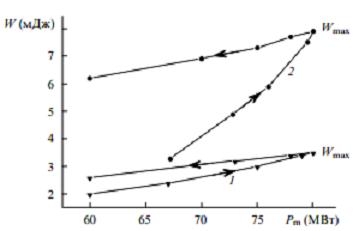
Рис.6. Зависимости энергии W лазеров на N₂ (1) и смеси N₂ - SF₆, (2) от мощности Р_m, выделяемой в момент достижения максимума напряжения на разрядном промежутке (p_SF6 = 20 мм рт.ст.).

 

 

Физический смысл Р_max - это Р_m при U_m = U₀/2, что означает возникновение согласованного режима накачки, при котором выполняется условие R(t_m) = Z (рис. 1.б).
Следовательно, при согласованном режиме накачки энергия генерации должна быть максимальна (W_max ). В исследуемых смесях максимум W действительно наблюдался при таких давлениях газов, когда максимальное напряжение разряда было равно 20 кВ, т.е. при U_m = U₀/2 (рис.3,4). В этом случае одновременно достигаются максимальные пиковая мощность накачки и электронная температура в разряде.
Разный наклон кривых на рис. 6 до и после максимума W обусловлен неодинаковой долей энергии, вкладываемой в разряд до и после максимума напряжения, которая растет с ростом p_N2 .Что касается существенного увеличения энергии генерации в смеси с добавками SF₆,то оно объясняется эквивалентным увеличением времени спада напряжения на плазме, которое также приводит к повышению энергии накачки, вкладываемой в разряд после максимума напряжения.
Полагая, что W_max= К(Р_max - Р_min ), где К – тангенс угла наклона кривых рис.6 на участке подьема W, a P_min - минимальная мощность, при которой возникает генерация, можно определить соответствующие параметры: К₁ = 7*10^-11 с, Р_1min = 33 МВт для азота и К₂ = 4*10^-10 с, Р_2min = 60 МВт для смеси N₂ - SF₆. Из результатов наших экспериментов легко найти КПД азотного лазера:

 

η = (W_max  / W₀ ) 100 % = К(1/2ZC - Р_min  / W₀  ) 100 %,    (3)

 

где W_max = К(Р_max - Р_min), Р_max = U₀²/4Z, W₀ = CU₀²/2 - энергия, запасенная в эквивалентной емкости С высоковольтного генератора. Подставляя в (3) численные значения параметров U₀ = 40 кВ, С = С₁ /2 = 10 нф, Z = 5 Ом, а также К и Р_min, получаем η₁= 0,04 % для N₂ и η₂ = 0,1 % для смеси N₂ - SF₆.
Следует отметить, что в ряде наиболее интересных для практики случаев - η₁ ≥  0,1 % и W₀ ≥  10 мДж - вторым слагаемым в (3) можно пренебречь. Тогда η ≈ K/2ZC. Параметр ZC характеризует длительность разряда генератора накачки.
Ранее считалось [5], что накачка N₂- лазера происходит только на стадии быстрого спада напряжения на плазме, поэтому в них стремились сделать минимальной лишь индуктивность L_d в контуре разряда обостряющей емкости через РП, включая индуктивность подвода. Из результатов настоящей работы следует, что в действительности основная часть энергии накачки вкладывается вблизи максимума напряжения на плазме. При этом согласно формуле (3) КПД η зависит от параметра ZC.
Обычно генераторами накачки N₂- лазеров служат линии Блюмляйна, генераторы Фитча или эквивалентные им схемы с двумя колебательными контурами типа схемы рис. 1 а. Для передачи максимальной мощности и энергии в нагрузку необходимо, чтобы емкости в обоих контурах были одинаковыми [11].                               

В этих условиях ZC = (2(L_z/C))^1/2C = (2(L_zC))^1/2, где L_z = L_g + L_d - суммарная индуктивность схемы возбуждения, L_g - индуктивность генератора накачки, включая индуктивность разрядника. Из формулы (3) следует, что при значительном снижении С необходимо повышение U₀. Однако в большинстве случаев это недопустимо, поэтому для существенного увеличения η принципиальное значение имеет минимизация суммарной индуктивности L_z. Оценки по формуле (3) показывают, что, например, для N₂- лазера без добавок SF₆ при η ≥ 0,5 % и типичных параметрах W_вых = 10 мДж, U₀ = 20 кВ необходимо обеспечить L_z ≤ 1,5 нГн.
Эти условия можно реализовать в схеме генератора Блюмляйна с многоканальным псевдоискровым разрядником (зарядное напряжение 10 кВ, разрядный ток 15 кА, индуктивность 0,5 нГн), подобным описанному в [12]. Если при этом активную среду возбуждать скользящим разрядом по поверхности диэлектрика [13], а в линии Блюмляйна использовать дистиллированную воду, то, как показывают оценки, можно получить L_z ≈ 1,5 нГн. Дальнейшее наращивание энергии излучения возможно лишь за счет увеличения зарядного напряжения, коммутируемого разрядником. Вместе с тем в большинстве традиционных конструкций N₂- лазеров суммарная индуктивность L_z » 1,5 нГн, чем и объясняется их низкая эффективность (например, в схеме рис. 1 а L_z = L_2s + L₃ = 11З нГн + 6 нГн ).
В заключение рассмотрим результаты работы [14], где описан N₂-лазер с магнитной схемой сжатия импульса накачки и где, как утверждается авторами этой работы, была получена энергия УФ излучения 20 мДж при η = 0,43 %. Пользуясь данными [14] и формулой (2), нетрудно оценить, что реальная эффективность в данном случае не может быть больше 0,12 %. Авторы [14] объясняют столь высокие характеристики излучения достигнутым параметром Е/р = 170 - 200 В/см*мм рт.ст. (p_N2 = 170 - 100 мм рт. ст.), полученным в результате применения схемы возбуждения с ультракоротким фронтом напряжения - 10 нс. Чтобы проверить это предположение, нами была создана схема накачки N₂- лазера с двумя контурами магнитного сжатия импульса напряжения, аналогичная описанной в [14]. Для этого в схему рис.1 последовательно дросселю L₂ добавлялась C₃L₃ - цепочка. Электрическая схема лазера показана на рис.7. Насыщающийся дроссель состоял из трех параллельно включенных индуктивностей на ферритовых сердечниках с общим сечением S = 29 см², C₃ = 5 нФ, С₁ = С₂ = 20 нФ, С₀ = 5 нФ.

 

 

 

 

 

 

 

 

 

 

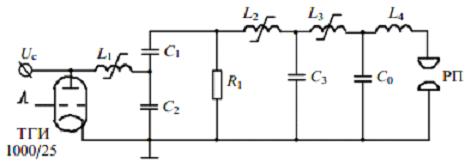
Рис.7. Электрическая схема лазера с двумя магнитными звеньями сжатия импульса напряжения.

 

 

 

На рис. 8 показан типичный импульс напряжения на РП. Длительность его фронта не превышала 20 нс, а отношение Е/р в разряде достигало 170 В/см* мм рт.ст. (p_N2 = 50 мм рт.ст.).

 

 

 

 

 

 

 

 

 

 

 

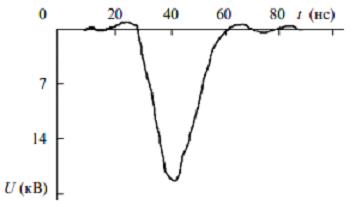
Рис.8. Осциллограмма импульса напряжения на РП при разряде в N₂ (схема рис.7) при р_N2 = 50 мм рт. ст., U_с = 27 кВ.

 

 

 

Однако необходимость использования ферритовых сердечников с большой площадью сечения не позволила сделать L_3s. (индуктивность третьего контура при насыщении L₃) существенно меньше L_2s. К тому же возросли потери на перемагничивание L₃ и из-за неравенства ударной емкости С₁/2 и емкости С₃ уменьшилась эффективность передачи энергии между ними [11]. Вследствие этого заметного роста мощности накачки и энергии излучения при использовании схемы рис.7 по сравнению со схемой рис.1 а не наблюдалось. Из полученных результатов следует, что схемы магнитного сжатия энергии неоптимальны для N₂- лазеров, поскольку их дроссели имеют довольно большую индуктивность обмоток. По-нашему мнению, данные работы [14] завышены и требуют дополнительного анализа.
Таким образом, в настоящей работе показано, что отношение Е_m/р в разряде не оказывает непосредственного влияния на характеристики N₂- лазера. Эффективность лазера зависит от параметров ZC, W₀, P_min , где Z- эквивалентное сопротивление схемы возбуждения, С - эквивалентная емкость высоковольтного генератора, W₀ - запасенная в ней энергия, P_min - пороговая мощность возбуждения. Энергия излучения пропорциональна мощности накачки, выделяемой в момент достижения максимума напряжения на плазме. Максимальная энергия генерации наблюдается при таком давлении газов, при котором согласованный режим накачки реализуется при максимальном напряжении на плазме.

 

 

 

1. Singh J.P., Thankur S.N. J. Sci. Industr. Res.. 25. 341 (19801.
2. Hariri A., Tarkashvand М., Karami A. Meas.Sci.Technol. 1. 659  (1990).
3. Vazquez Martinez A., Aboitcs A. IEEE J.Guantum Electron. 29. 2364(1993).
4. Godar B. IEEE J,Quantum Electron. 10. 147 (1974).
5. Месяц Г.А., Осипов B.B., Тарасенко В.Ф. Импульсные газовые  лазеры (М.. Наука. 1991).
6. Fitzsimmons W.A., Anderson L.W., Riedhauser С.Е., Vrtiler J.M. IEEE J.Quantum Electron. 12. 616 (1976).
7. Вартапетов C.K. ЖТФ. 56. 1387 (1981).
8. Ломаев М.Л., Тарасенко В.Ф., Верховский B.C. Электрон. техн. Сер.11, вып.1. 58 (1991).

9. Буранов С.Н., Горохов В.В., Карелин В.И., Репин П.Б. Квантовая электроника. 17. 161 (1990).
10. Афанасьев Б.П., Гольдин O.Е., Коляцкин И.Г., Пинес Г.Я.  

        Теория линейных электрических цепей (М.. Высшая школа. 1973).

11. Persephonis P., Giannetas В., Parthenios J., GeorgiadesC., loanov А. IEEE J. Quantum Electron.. 29.2371 (1993).
12. Mechtersheimer G., Kohler R. J.Phys. E. 20. 270(1987).
13. Брызгалов П.П., Карлов H.B., Ковалев И.О., Кузьмин Г.П. Квантовая электроника. 15. 1971 (1988).
14. Seki Н., Takemori S., Sato Т. IEEE J. Sel. Top. in Quantum  Electron. 1,825 (1995).